山村ドレススタジオ >
テキスト > 「立体にする」とはどういうことか
「立体にするとは?」、と問うと、粘土細工や彫刻など、素材や技術的な違いにより、具体的な手順や考え方は様々だが、ここでは、「平面の素材を、特定の形に切り離して立体にする」こと、つまり、「洋服の型紙をつくるときの考え方」についてのみに限定して考えることにする。
紙を切り取って組み立てる立体工作や、木の板を切って組み立てる家具なども、考え方としてはほぼ同じだ。
たとえ、「平面の素材を、特定の形に切り離して立体にする」、と限定したところで、考え方は無限にあるだろうが、ここでは大きく、「立体をイメージしてみる」、という考え方と、「立体をすべて測ってみる」、という二つの考え方に分け、それぞれについて検討してみる。
その前にまず、【1】の展開図を見てもらいたい。これらの展開図を立体にすると、どのような形になるだろうか?
-
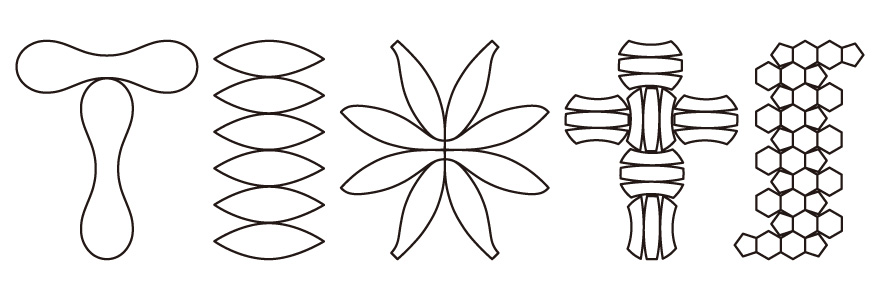
【1】
その答えは、すべて「球体」である。
-
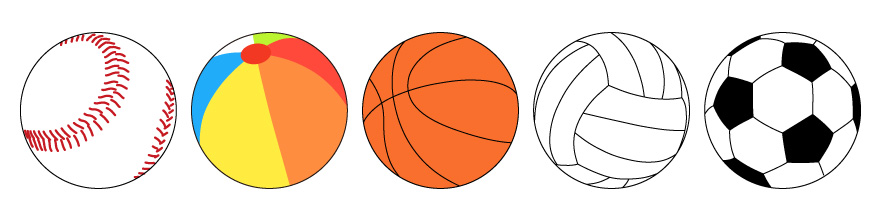
【2】
厳密には、野球のボールなどは、中から圧力をかけなければ球体にはならないが、これらは、同じ形にするためのアプローチはいくらでもあることを示している。
【3】の展開図を見てもらいたい。 この展開図を立体にすると、どのような形になるだろうか?
 【3】
【3】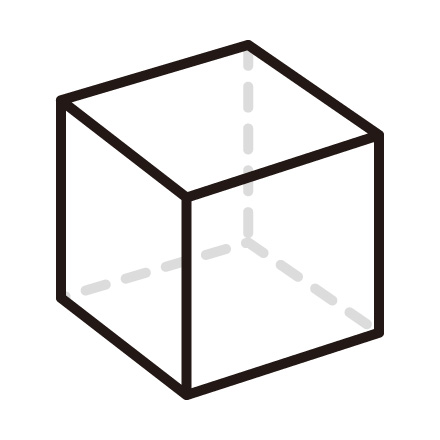 【4】
【4】
この問いに関しては、実際に組み立てた経験や、過去に同じ形を見て記憶している可能性もあるが、結果、【4】のようなサイコロ型(正六面体)になる。
ただ、ここでは、「どのような形になるのか?」、という答えではなく、「どのようして考えたのか?」、について考えていっててほしい。>
続いて、【5】の写真のゾウのぬいぐるみ。
 【5】
【5】
このゾウのぬいぐるみの側面の型紙は、【6】のような形になっている。
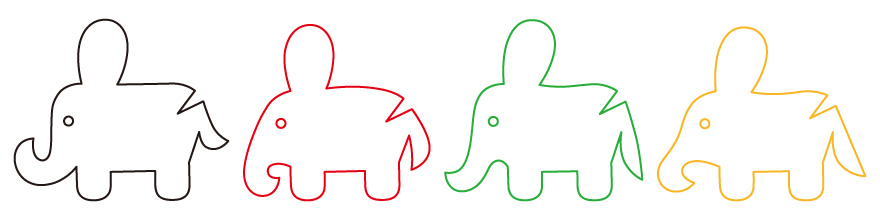 【6】
【6】
これらの型紙を重ねてみると、【7】のようになる。
 【7】
【7】
これらは、まず一体目を作り、その後にバリエーションとして増やしたものだが、ここで強調しておきたいことは、バリエーションをつくるときに、「ここの長さは、元の形の、○○倍にしよう」だとか、「この部分は、プラス何ミリにしよう」といった、計算式を含めて、数字では考えていないことで、「鼻をを、もうちょっと曲げよう」だとか、「今度は、少し丸い感じにしよう」といったように、かなり感覚的にバリエーションの型紙を増やしていったことだ。
【8】は、現在出回っているバレーボールの型紙を、私が想像して作ったものだが、この型紙の形を想像してもらいたい。
また、このバレーボールは、何種類で何枚の部品で構成されているだろうか?
 【8】
【8】
実際のバレーボールの型紙の形は不明だが、【9】ような構造になっており、型紙の各部品は、1種類8枚で構成され、それぞれの部品は、【10】ような形となる。
 【9】
【9】 【10】
【10】
ここでも考えてもらいたいことは、これらが、「どのような形か?」、という答えではなく、「どのように考えたのか?」、ということであり、どのように考えたのかを考えてみてほしい。
以前、この問いを出したとき、「勘」だと言った学生がいたが、そんなところだと思う。
これらの「立体をイメージしてみる」というアプローチから言えることは、作図(型紙をつくること)とは、「デッサン」に近いのではないか、ということだ。
「デッサンに近い」ということは、出来上りの立体から想像した型紙の形を、だいたいでも構わないので、とりあえず描いてみて、それを修正して検証する。そして、そのことを繰り返して、徐々に精度を高めていき、それらの過程で型紙をデッサンするように「描いていく」、という考え方で、ここでは「絵」としての調和がとれているか、あるいは「絵」として美しいかが判断基準となる。
【11】は、【1】【2】の図から抜粋したものだが、ビーチボールの形について考えてみる。
 【11】
【11】
では、このビーチボールの型紙が、どのような条件を満たせば、楕円形やラグビーボールなどのような形ではなく、正確な球形になるだろうか?
詳細には様々な条件がありうるが、ここでは【12】で示した2点をあげてみる。
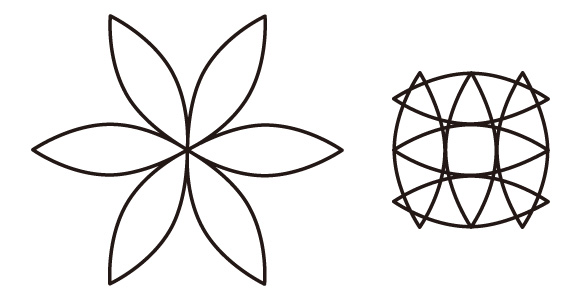 【12】
【12】
一つは、部品が合わさる頂点の部分が、角にならないためには、その全体の角度が360度でなければならず、このビーチボールは6枚の部品で構成されているため、各部品の角は、360÷6=60度にする必要がある。
もう一つは、球形であるということは、経度方向と緯度方向が、同じ長さでなければならず、その条件を満たすためには、各部品の縦横の長さの比率を、1対3の関係にする必要がある。
そのような条件を満たすため、これらは、立体をイメージして 自由に「描く」のではなく、計算どおりに「書く」ことになる。
【13】の左は、定番のサッカーボールで、右のようなデザインのものもあるのだが、左のボールのデザインを右のように変更する手順を考えたい。
 【13】
【13】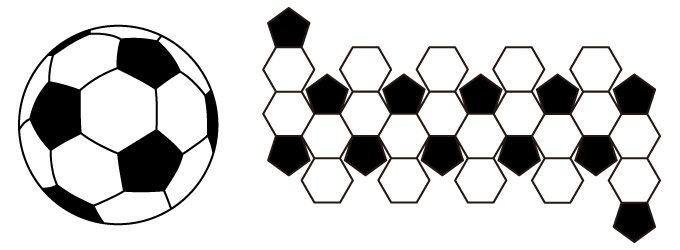 【14】
【14】
【14】は、【1】【2】と同じ、サッカーボールの部品の構成を示した展開図である。
このサッカーボールの、五角形と六角形の一組を取り出して、考えてみる。
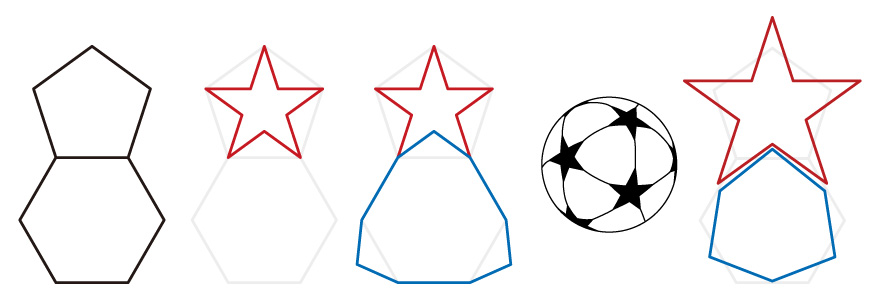 【15】
【15】
【15】の左から、(1)五角形と六角形を並べたもので、(2)この五角形を星型にした状態、(3)それだけだと五角形の部分の小さな5か所の三角形が欠けたままなので、六角形の部品に三角形を追加した状態である。
それだけでも、【13】の右のボールに近いものになるのだが、星が小さい(4)。
そこで、六角形から変更された九角形の、もともとの二か所の角の部分が一か所になるよう長さの関係を調節し、それに合わせて星型を大きくする。(5)
 【16】
【16】
このような手順を論理的に進めれば、【13】の左から右への変更が可能となる。
では、【17】の、左から右への変更は、どのようにすれな可能になるだろうか?
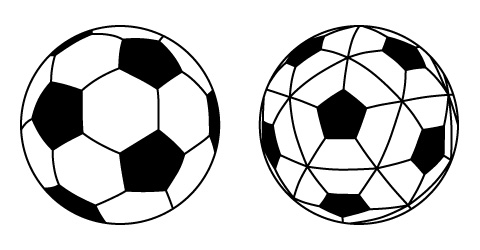 【17】
【17】
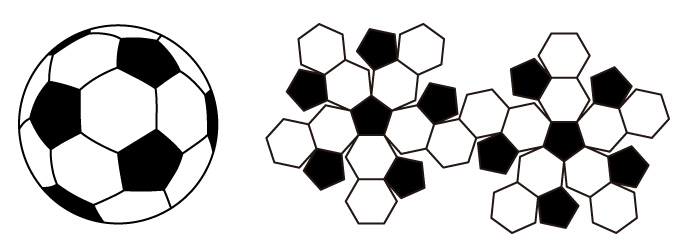
【18】は、【14】の展開図と、出来上る立体に違いはなく、配置を替えただけのもので、【19】は、【17】の右のボールの展開図で、同じような配置で部品の構成を示すことが可能だ。
したがって、【17】の双方のボールは、正十二面体の変形だと考えることができる。
 【18】
【18】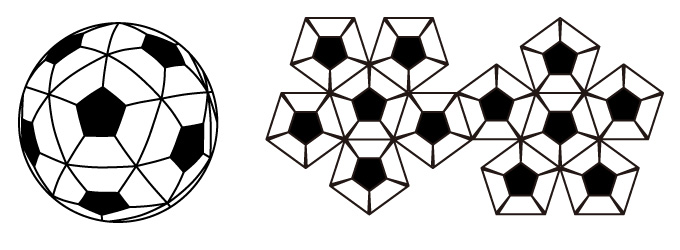 【19】
【19】
しかし、左から右に理論的に変更する方法はなかった。
【13】よりも、【17】の方が、双方のデザインが似ている印象もあるが、一見して似ているように見えることと、理論的な変更が可能かということは、必ずしも一致しない例だといえる。
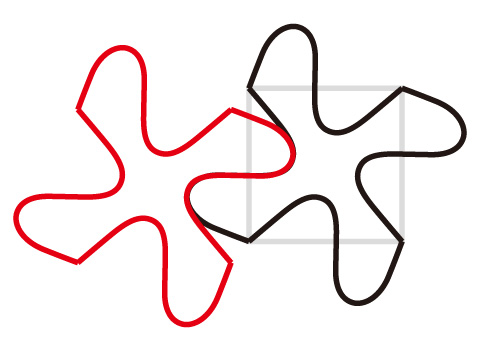
【20】の左は、【3】【4】と同じもの、右は、正面の四角形の高さを4分の3にしたものであるが、この右の立体の展開図が、どのような形であるかを、考えてもらいたい。
※赤い線を元の立方体、黒い線を目標とする立体とする。
※立体の右下に見える面を正面とする。
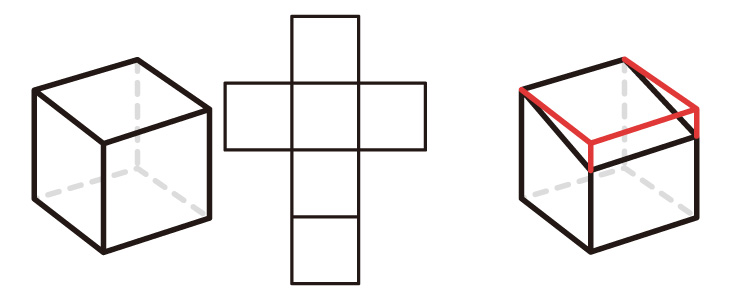 【20】
【20】
正解は、【21】のようになるのだが、繰り返しになるが、ここでも考えてもらいたいことは、「どのような形になるのか?」、という答えではなく、「どのようして考えたのか?」、である。
 【21】
【21】
【20】で行ったような変更を、より複雑にしたものが、【22】であるが、変更するためのルールは同じで、そのルールに従って順番に変更すれば、ほとんどの場合、変更は可能である。
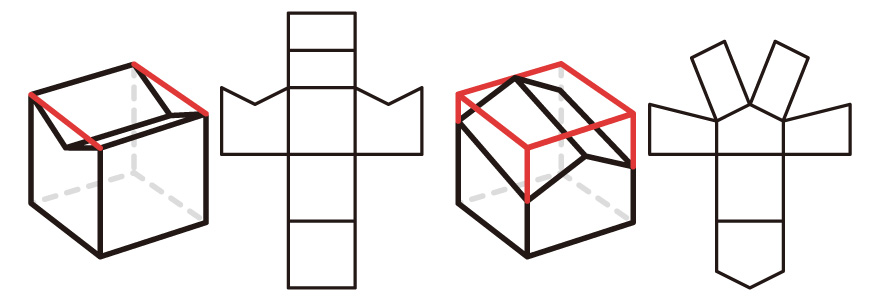 【22】
【22】
その共通のルールとは、【21】では正面、【22】の左は左右の面、【22】に右は正面とその反対の面を規準面として、最初にその規準面を変更し、その面にあるそれぞれの辺の長さと、合わせる面にある辺の長さを同じにする、ということだ。
あとは、この作業を全ての辺において繰り返すとよい。
ただし、このルールだけでは、【22】の右の図の上側の2つの細長い長方形の変更が不可能で、実際にはこの形は平行四辺形なのだが、どのくらい歪んだ形なのか分からず、この場合は対角線の長さを測る必要がある。
こちらは少し「立体を全て測ってみる」という考え方とは違ってくるが、【23】の写真を見てもらいたい。
このようなサッカーボールも実際にあるのだが、型紙は【8】のバレーボールと同じく、私が想像してつくったものだ。
 【23】
【23】
このサッカーボールの型紙は、【24】のようになった。
この形をよく観察すると、角の部分を結んだ線が、正方形であることが分かる。
正方形だということは、このサッカーボールは、同じ部品が6枚で構成されているので、正六面体(サイコロ型)の変形であるということだ。
 【24】
【24】 【25】
【25】
しかし、正六面体の変形だとすると、正方形を3枚合わせて、その角は90度×3=270度となり、平らな状態にはならない。
そこで、各辺の直線を大幅に蛇行させ、S字カーブとすると同時に、それぞれの角を360度÷3=120度に変更している。
 【26】
【26】
これらの「立体を全て測ってみる」、というアプローチから言えることは、作図(型紙をつくること)とは、「折れ線グラフ」に近いのではないか、ということだ。
では、「折れ線グラフに近い」とは、どのようなことだろう?
それは、以下のように、それぞれの箇所の長さ(角度)を測って、全てに「点」を記し、それらの点を結んでゆけば、必ず目的の形に到達する、という考え方で、こちらは理論の蓄積や、正確さがものを言う。
この、「立体をイメージしてみる」、「立体をすべて測ってみる」、という二つの考え方を、洋服の型紙を作ることとして考えると、「立体裁断」と、「原型作図」という型紙の作成方法とも関連してくるが、これらはあくまで「考え方」の話であり、俗に言う、「右脳思考」「左脳思考」の捉え方に近い。
実際に服の型紙を作る場合、前者の「イメージする」という感覚的な考え方だけでは、デッサンの技術だけで型紙を作ろうとするようなもので、「服は作れない」だろう。あるいは、服が作れたとしても、とても効率が悪い。
一方、後者の「全て測ってみる」、という理論的な考え方だけで、服を作ることは出来るだろうが、数字のみを追うことになり、美的感性の入る余地がなく、あまり「良い服にはならない」、のではないかと思う。
したがって、これらは、「同時」に、あるいは「交互」に考えるのが望ましい。
人が、「難しい」と感じることには、「難易度が高い」ことの他に、あと「時間がかかる」ことがあるように思うが、この両者は対策方法が全く異なる。
おそらく、「立体をイメージしてみる」ことは、苦手な人は、「難易度が高い」と、感じることもあるはずだが、「立体をすべて測ってみる」ことは、時間をかければ、ほとんど誰にでもできることで、かけられる時間があるかどうかが問題となるはずだ。
これらは、作り手の得手不得手もあると思われるので、得意な方から始めればよいことだし、また、「どのようなものを作るのか」による違いも関係してくるので、柔軟に考えていけばよいと思う。



 【3】
【3】 【4】
【4】 【5】
【5】 【6】
【6】 【7】
【7】 【8】
【8】 【9】
【9】 【10】
【10】 【11】
【11】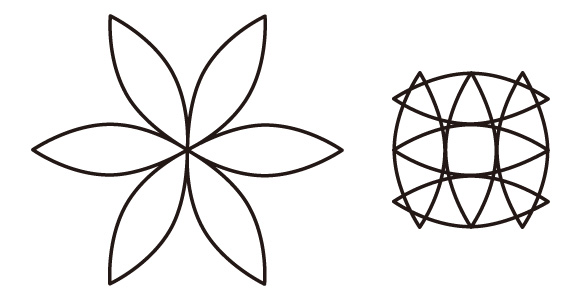 【12】
【12】 【13】
【13】 【14】
【14】 【15】
【15】 【16】
【16】 【17】
【17】 【18】
【18】 【19】
【19】 【20】
【20】 【21】
【21】 【22】
【22】 【23】
【23】 【24】
【24】 【25】
【25】 【26】
【26】 【27】
【27】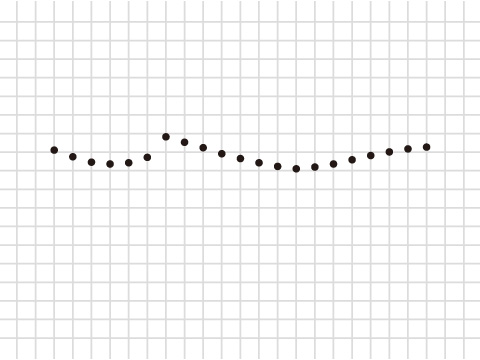 【28】
【28】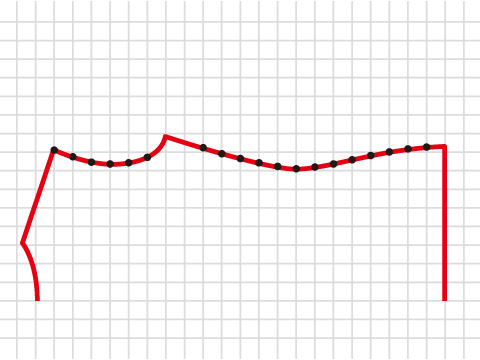 【29】
【29】